Plastic Analysis and Design

Plastic Analysis

The easiest but difficult to remember topic for me was this. LOL.

Civil Engineering deals with daily stuff and you can see what your field has worked on such as roads, bridges, pathways, transit systems, buildings you see and live in, and many more. Nowadays we have to consider earthquake loading in most of the structures and plastic analysis and design play an important role when studied in depth.

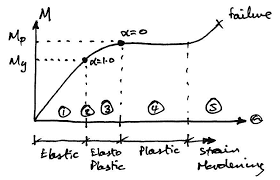
The plastic analysis is used to check the collapse behavior of the structure with an increase in yield of cross-section increasing with increase in load. This analysis gives a significantly higher value for failure load for the safety of the building when compared to elastic load capacity.

With this, we come across the term as plastic moment and hinge. The theoretically maximum moment which the section reaches in a plastic hinge is the plastic moment. The plastic hinge is said where deformation takes place where the plastic moment takes place.

This plastic hinge is seen to have a larger rotation with the constant plastic moment and thus this acts as a damping device when an earthquake occurs.

I know I know this is a little confusing... refer to this...
Member > Bending (Deformation) > Moment Takes Place (Yield Stress Reached) > Plastic Hinge Is Formed (Takes Place In Yield Zone).

Now let's see points to be remembered and assumptions:

a. Plane transverse sections remain plane and normal to the longitudinal axis before and after bending.

b. Effect of Shear is neglected.

c. Material is homogenous and isotropic both in the elastic and plastic state.

d. Modulus of elasticity has the same value both in tension and compression.

e. There is no resultant axial force in the beam.

f. The cross-section of the beam is symmetrical about an axis through its centroid and parallel to the plane of bending.

Plastic Design

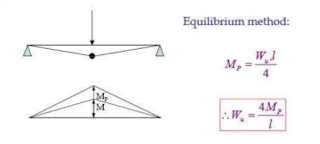
Now how to calculate collapse load?

The basic need is,

Plastic Moment, Length of Plastic Hinge, and Collapse Load.

For Length of Plastic Hinge:

Concentrated Load,

Lp=L/3 (Rectangle) =L/8 (I Section)

for other shapes, we need Shape Factore (ɑ),

Lp=L(1-1/ɑ)

UDL Loading,

Lp=L.sqrt(1-1/ɑ)

Shape Factor:

Aplha=Mp/My=Zp/Z

where Mp is plastic moment

           My is yield moment

           Zp is plastic elastic modulus

                 Zp= A/2(Z1+Z2)

           Z is elastic modulus

Shape factor (ɑ) that should be remembered:

Rectangle = 1.5

Triangle    = 2.346 (Highest)

Circular    = 1.697

Diamond  = 2

Simply Supported Beam

Fixed Beam

The formula for many sections and loading conditions can be studied.